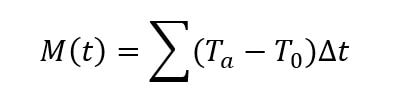Concrete Maturity Formula
ASTM C1074 defines two methods of calculating concrete maturity which are referred to as "maturity functions." The objective of each maturity function is to combine time and temperature into a single "maturity" number that can be correlated to concrete strength at any particular time. The following is a brief summary of the two formulas for educational purposes. Refer to ASTM C1074 for actual specifications.
temperature-time factor (Nurse-Saul method)
The most popular maturity function used in the United States is the temperature time factor method, also known as the Nurse-Saul method. Of the two methods, the temperature-time method tends to be the more conservative method, meaning that at higher temperatures it tends to underestimate concrete strength. Since there is little that happens in the field to increase concrete strength, but there are a lot of ways to decrease concrete strength, this conservative approach is often preferred.
The time-temperature factor is calculated over time as follows:
The time-temperature factor is calculated over time as follows:
where:
M(t) = the temperature-time factor (maturity), usually with units of °C-Hrs
Δt = the time interval between time steps, usually units of Hrs
Ta = the average concrete temperature during the time step, always in °C
To = the datum temperature, always in °C
Note that if Ta is less than To, the maturity change during that time step is zero.
DATUM TEMPERATURE
The datum temperature in this function is important because this number quantifies the effect of temperature on the rate of maturity gain. For example, if the concrete is 10C hotter, how much faster does it gain maturity? A standard rule-of-thumb is that chemical reaction rates generally double with each 10 °C increase in temperature, and the reaction speed is cut in half for each 10 °C decrease in temperature.
For Type I cement (without admixtures) and a moderate range of curing temperatures (0 to 40 °C), ASTM C1074 recommends using 0 °C as the datum temperature. As a result:
Although seldom done in practice, a more accurate, and usually more "aggressive" datum temperature can be determined by generating calibration data at multiple temperatures and fitting a line to the resulting data. This procedure is outlined in ASTM C1074.
M(t) = the temperature-time factor (maturity), usually with units of °C-Hrs
Δt = the time interval between time steps, usually units of Hrs
Ta = the average concrete temperature during the time step, always in °C
To = the datum temperature, always in °C
Note that if Ta is less than To, the maturity change during that time step is zero.
DATUM TEMPERATURE
The datum temperature in this function is important because this number quantifies the effect of temperature on the rate of maturity gain. For example, if the concrete is 10C hotter, how much faster does it gain maturity? A standard rule-of-thumb is that chemical reaction rates generally double with each 10 °C increase in temperature, and the reaction speed is cut in half for each 10 °C decrease in temperature.
For Type I cement (without admixtures) and a moderate range of curing temperatures (0 to 40 °C), ASTM C1074 recommends using 0 °C as the datum temperature. As a result:
- The maturity function does not increase in maturity at 0 °C or colder, which is a good assumption considering that the concrete is most likely frozen.
- At the calibration temperature (e.g. 20 °C) the rate of maturity increase will be perfectly accurate because it matches the calibration temperature.
- At 40 °C the rate of maturity increase is twice that at the calibration temperature.
- At temperatures over 40 °C, the time-temperature method with a 0C datum will underestimate the actual maturity. This results in an underestimate of concrete strength and adds a desirable margin of safety to the calculation
Although seldom done in practice, a more accurate, and usually more "aggressive" datum temperature can be determined by generating calibration data at multiple temperatures and fitting a line to the resulting data. This procedure is outlined in ASTM C1074.
Equivalent Age (Arrhenius)
The equivalent age method is a more aggressive, and can be a more accurate method than the temperature-time method over a wide range of concrete curing temperatures. That said, one needs to be careful to not make assumptions that would result in an overestimate in concrete strength. But in applications where time is of the essence, equivalent age is a valuable tool.
Equivalent age is calculated as follows:
Equivalent age is calculated as follows:
where:
te = the equivalent age in days or hours
Q = the activation energy divided by the gas constant (Ea/K)
Ta = the average temperature of the concrete during the time step in K
Ts = the specified (reference) temperature in K
Δt = the time step in days or hours
As opposed to the linear temperature-maturity relationship provided by the temperature-time factor method, the temperature-maturity gain relationship for the equivalent age method is exponential. This can result in an extremely high rate of indicated strength gain at elevated temperatures (e.g. > 60 °C/140 °F) but leaves a smaller margin of safety.
Typical values of activation energy range from 38,000 to 45,000 which results in a Q value of 5000K, and traditional values of Ts are 20 and 23 °C. But for the most accurate results one should experimentally determine the appropriate values for the specific mix design using procedures defined in ASTM C1074.
te = the equivalent age in days or hours
Q = the activation energy divided by the gas constant (Ea/K)
Ta = the average temperature of the concrete during the time step in K
Ts = the specified (reference) temperature in K
Δt = the time step in days or hours
As opposed to the linear temperature-maturity relationship provided by the temperature-time factor method, the temperature-maturity gain relationship for the equivalent age method is exponential. This can result in an extremely high rate of indicated strength gain at elevated temperatures (e.g. > 60 °C/140 °F) but leaves a smaller margin of safety.
Typical values of activation energy range from 38,000 to 45,000 which results in a Q value of 5000K, and traditional values of Ts are 20 and 23 °C. But for the most accurate results one should experimentally determine the appropriate values for the specific mix design using procedures defined in ASTM C1074.
Temperature-Time |
Equivalent Age |
|
Also known as |
Nurse-Saul Method |
Arrhenius Method |
Maturity Units |
°C-Hrs |
Eq. Hrs/Days |
Benefits |
Simple Conservative strength estimates Common in the U.S. |
Can be ore accurate Aggressive strength estimates More engineering supervision recommended |
Maturity rate vs temperature parameter |
Datum temperature in °C |
Ea/R in K |